Objective and use case
What you’ll build: A simple LC high‑pass filter for basic RF (tens of kHz to a few MHz) with a signal source and a resistive load, and you’ll measure its frequency response.
What it’s for
- Filtering low‑frequency noise (50/60 Hz hum) on a low‑power RF line.
- Separating the signal from a small antenna from the slow noise generated by the power supply.
- Pre‑filtering the input of a homebrew AM receiver to reduce audio interference.
- Cleaning up the output of an RF generator before amplifying it in the next stage.
- Measuring the real behavior of inductors (series resistance, parasitic capacitances) in a specific frequency band.
Expected result
- Very reduced output voltage for low frequencies (for example, 1 kHz: attenuation >20 dB with respect to the input).
- Output voltage close to the input for high frequencies (for example, >100 kHz: |Vout| > 0.9·|Vin|, depending on the values of L and C).
- Gain curve |Vout/Vin| that increases with frequency until it stabilizes near 1 (0 dB) in the passband.
- Measurable cutoff frequency where |Vout| ≈ 0.707·|Vin| (−3 dB), consistent with the theoretical value calculated from L, C, and the load resistance.
Target audience: RF hobbyists, analog electronics and radio students; Level: Beginner–intermediate (with basic notions of RLC and oscilloscope).
Architecture/flow: RF signal source → LC high‑pass filter (inductor + capacitor configured as a first‑order filter) → load resistor → measurement of Vout with oscilloscope or AC multimeter, sweeping frequency to obtain the gain curve.
Materials
- 1 × Function generator (able to reach at least 500 kHz or 1 MHz).
- 1 × Oscilloscope (preferably 2 channels, bandwidth ≥ 20 MHz).
- 1 × Inductor [L1] of 100 µH (or a nearby value between 47 µH and 220 µH).
- 1 × Capacitor [C1] of 1 nF (ceramic, preferably NP0/C0G type for basic RF).
- 1 × Resistor [R1] of 1 kΩ (¼ W).
- 1 × Breadboard (test board).
- 4–6 × Male‑male jumper wires.
- 1 × Power supply for the generator (if it does not have an internal one).
- 1 × Clip or cable for the oscilloscope GND reference.
(You can adjust the values of L1 and C1; the goal is for the cutoff frequency fc ≈ 1 / (2π·√(L·C)) to fall in a range where your generator and oscilloscope operate comfortably.)
Wiring guide
- Connect the ground (GND) of the function generator to the GND reference of the breadboard.
- Connect the GND clip of the oscilloscope to the same GND point on the breadboard.
- Connect the signal output of the generator (Vin) to a node on the breadboard that we’ll call VIN node.
- Connect channel 1 of the oscilloscope (CH1) to the VIN node to view the input signal.
- Connect the inductor [L1] between the VIN node and a new node that we’ll call VOUT node.
- Connect the capacitor [C1] between the VOUT node and GND.
- Connect the resistor [R1] between the VOUT node and GND (this will be the load of the filter).
- Connect channel 2 of the oscilloscope (CH2) to the VOUT node to view the output signal.
- Verify that there is no other component or wire directly connecting VIN node to GND or VOUT node to VIN node without going through [L1], nor to GND without going through [C1] or [R1].
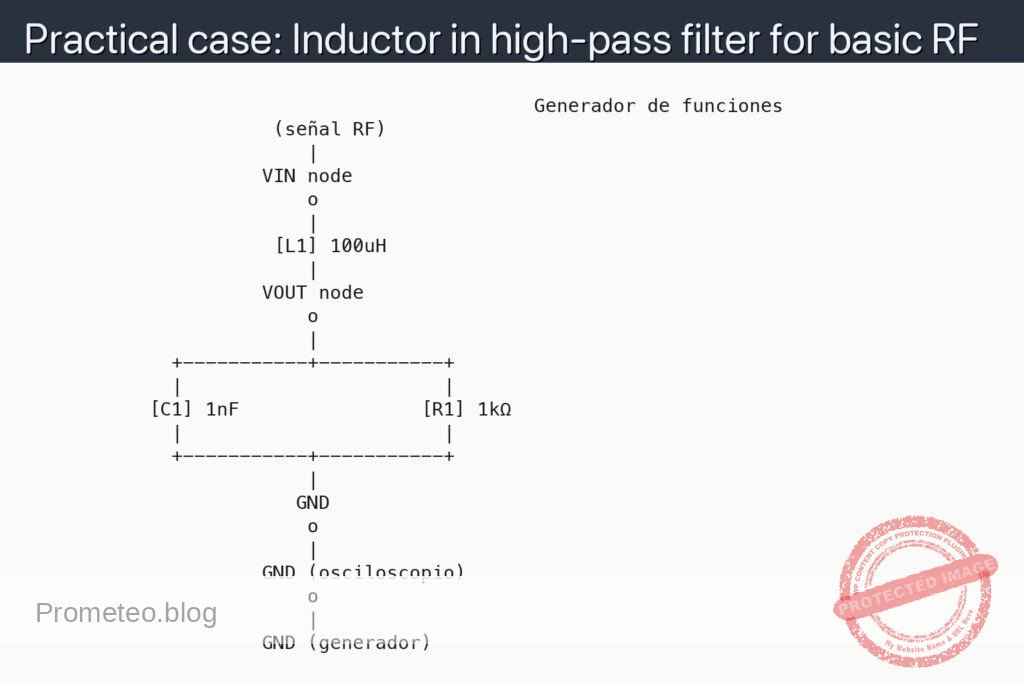
Schematic
Generador de funciones
(señal RF)
|
VIN node
o
|
[L1] 100uH
|
VOUT node
o
|
+-----------+-----------+
| |
[C1] 1nF [R1] 1kΩ
| |
+-----------+-----------+
|
GND
o
|
GND (osciloscopio)
o
|
GND (generador)
Measurements and tests
-
Initial setup:
- Set the function generator to a sine wave of 1 Vpp amplitude (peak‑to‑peak) and 0 V offset (centered at 0).
- Connect CH1 of the oscilloscope to the VIN node and CH2 to the VOUT node, both referenced to GND.
- Configure the oscilloscope to see both signals superimposed (dual mode or XY mode if you want to compare phase).
-
Measurement of input amplitude (Vin):
- Adjust the CH1 scale so that the sine wave occupies a good portion of the screen.
- Measure the input amplitude, which we’ll call V_in_pp (input peak‑to‑peak voltage): it is the difference between the maximum peak and the minimum peak of the signal on CH1.
- Verify that V_in_pp remains approximately constant (for example, near 1 Vpp) when changing the frequency on the generator.
-
Measurement of output amplitude (Vout):
- Observe the CH2 signal and measure its peak‑to‑peak voltage, which we’ll call V_out_pp.
- Calculate the magnitude gain as |H(f)| = V_out_pp / V_in_pp.
- For greater accuracy, use the oscilloscope’s automatic measurement functions (Vpp measurement on each channel).
-
Frequency sweep:
- At low frequency (for example, 1 kHz):
- Set the generator to 1 kHz.
- Measure V_in_pp and V_out_pp. You should observe V_out_pp much smaller than V_in_pp.
- Near the theoretical cutoff frequency:
- Calculate the approximate cutoff frequency of the series‑parallel LC filter:
- fc ≈ 1 / (2·π·√(L·C)).
- With L1 = 100 µH and C1 = 1 nF ⇒ fc ≈ 503 kHz (approx.).
- Set the generator to frequencies around this value (for example, 100 kHz, 300 kHz, 500 kHz, 700 kHz, 1 MHz).
- At the frequency where V_out_pp ≈ 0.707·V_in_pp, you are approximately at the cutoff frequency (−3 dB).
- At high frequency (for example, > 1 MHz if your equipment allows it):
- Increase the frequency up to where your generator and oscilloscope work well (without too much distortion or loss).
- Measure V_out_pp; it should approach V_in_pp, that is, |H(f)| ≈ 1.
- At low frequency (for example, 1 kHz):
-
Measurement in dB (optional but recommended):
- The gain in decibels (dB) can be obtained with:
- Gain_dB = 20·log10(V_out_pp / V_in_pp).
- At low frequencies, large negative gain values in dB are expected (for example, −20 dB, −40 dB…), indicating strong attenuation.
- Around the cutoff frequency, approximately −3 dB is expected.
- At high frequencies, the gain should approach 0 dB.
Interpretation of the inductor’s behavior in the filter
- At low frequencies:
- The inductor [L1] behaves almost like a short (its reactance XL = 2·π·f·L is small).
- The signal sees the path from input to output through the inductor, but it encounters C1 and R1 to GND that “shunt” the signal to ground.
-
The result is that little voltage appears at VOUT node: the filter attenuates low frequencies (high‑pass behavior).
-
At high frequencies:
- XL increases with frequency, so the inductor looks more like a “large resistor” (high impedance).
- The capacitor [C1] at high frequency behaves with low reactance (XC = 1/(2·π·f·C) decreases with frequency) and together with R1 sets a reference point for the output.
-
The output node VOUT node sees less shunting to GND relative to the signal path, allowing the output voltage to be close to the input.
-
Role of resistor [R1]:
- R1 acts as the load of the filter and as a DC reference for capacitor C1.
- Without R1, the output node could be “floating” under some conditions and it would be hard to measure a stable output.
- The value of R1 affects the shape of the frequency response (Q, slope); for this basic case we use 1 kΩ as a typical value.
Common mistakes
- Incorrectly connecting the GND reference:
- If the generator GND is not tied to the oscilloscope GND, you’ll see strange waveforms or significant noise.
-
Always tie all grounds to a single common point.
-
Reversing the circuit connections:
- Although the ideal LC filter would be reversible in some cases, for this educational case strictly follow:
- Generator → [L1] → VOUT → [C1 and R1] → GND.
-
Do not place the capacitor in series nor the inductor to GND; that would be another filter topology.
-
Using unsuitable inductors:
- An iron‑core inductor designed for 50/60 Hz can behave poorly in RF (losses, saturation, parasitic resonances).
-
Prefer small inductors, air‑core type or ferrite cores suitable for RF.
-
Using very long wires:
- At frequencies of hundreds of kHz or more, long wires introduce appreciable parasitic inductances and capacitances.
- Keep connections as short and tidy as possible so as not to distort the result.
Possible improvements and variants
- Changing the cutoff frequency:
- If you want a lower fc, increase L1 or C1 (or both).
- If you want a higher fc, decrease L1 or C1.
-
Always recalculate: fc ≈ 1 / (2·π·√(L·C)).
-
Measuring phase as well as amplitude:
- Use the XY mode of the oscilloscope or measure the time difference between zero‑crossings of Vin and Vout.
-
The phase will show how the output leads or lags the input depending on frequency.
-
Adding more stages:
-
You can place another identical high‑pass filter in cascade (output of the first to the input of the second) to obtain a higher attenuation slope (extra 2nd order).
-
Trying other waveform types:
- Use a square wave and observe how the filter attenuates the low‑frequency component, modifying the shape of the output signal.
- Reason in terms of harmonic content and how the filter allows the higher‑frequency components to pass more.
With this setup you will have carried out a simple but very illustrative practical case of using an inductor in a high‑pass filter for basic RF, relating theory (inductance, reactance, cutoff frequency) with real measurements on the oscilloscope.
More Practical Cases at Prometeo.blog
Find this product and/or books on this topic on Amazon
As an Amazon affiliate, I earn from qualifying purchases. If you buy through this link, you help maintain this project.
Quick quiz
More Practical Cases on Prometeo.blog